
1b shows a schematic category for modeling of permeability during solidification process. In the field of metallurgy, however, the models mentioned above had an important application in the mathematical modeling of flow through arrays of dendrites during the solidification of mushy alloys. Two categories of permeability models a) Common permeability model b) Metallurgical permeability model (solidification) Also McCartney (1994) calculated the permeability in the range of low Reynolds numbers up to about 150 by Lattice Gas Cellular Automat (LGCA) model. Particularly noteworthy is the work of Koch & Ladd (1997) for modeling permeability and drag force based on Reynolds number using a Lattice-Boltzmann formulation. Several authors computed the fluid flow through periodic arrays of cylinders as the function of Reynolds numbers for three ranges of low, moderate, and high Reynolds number ( Cai & Berdichevsky, 1993 Edwards et al., 1990 Eidsath et al., 1983 Ghaddar, 1995 Koch & Ladd, 1997 McCartney, 1994 Nagelhout et al., 1995 Sangani & Mo, 1994 Sangani & Yao, 1988 Thom & Aplelt, 1961). The effect of fluid inertia on pressure drop required to drive the flow is a function of Reynolds number. Analysis of permeability for Stokes flow through periodic arrays of cylinders were done by Sangani & Acrivos (1982), Sparrow & Loefler (1959) and, Larson & Higdon (1986).
EFFECT OF DENDRITE STRUCTURE FULL
Since it is not possible to solve analytically for this type of flow over the full range of porosities, two limiting closed form solutions are used for lubrication and point-particle (dilute) models in low and high porosities, respectively. A more realistic approach will be introduced that assumes geometry of a periodic or random array of cylinders. 1995 Williams et al., 1974) and an array of spaced particles. 1a two of the most commonly used geometries for analytical models are capillaries ( Carman, 1937 Chen et al. 1 presents two viewpoints for investigation of the permeability in the porous media: metallurgical view and non-metallurgical (or common) view.Īs shown in Fig. To obtain an expression for the permeability as a function of the porosity of the porous medium, one generally considers flow through an idealized medium geometry, since it is impractical to solve the flow equations for the complex flow between the particles. Interdendritic flow, in many CFD documents, is described using Darcy’s law, which relates the fluid flow rate to the pressure gradient, fluid viscosity, and permeability of the porous medium. In a great number of studies micro/macro solidification models have been simulated based on the permeability factor using Darcy’s law ( Ganesan & Poirier, 1990 Nandapurkar et al., 1991 Poirier, 1987 Worster, 1991). Therefore, formation of the micro-defects depends on controlling of the permeability factor. Herein, the region in the grain growth stage is introduced as a mushy zone (or porous media), where the solid phase is constantly progressing and the ability of fluid to flow into the mushy zone is known as permeability of interdendritic liquid. The micro-defects are located in the interdendritic space, which are micro-channels that fluid flow through them in the last stage of the solidification. Some critical defects such as micro/macro segregation, micro/macro porosities and micro/macro shrinkage take place in the solidification stage.
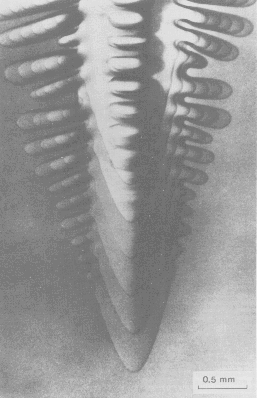
Subsequently, number, distribution and morphology (dendritic or non-dendritic) of the grains are formed during the solidification. Alloy solidification is a two stage process, which starts by nucleation and ends by growth of solid phases.


 0 kommentar(er)
0 kommentar(er)
